Leetcode problem 1105 filling-bookcase-shelves

Problem Description

We have a sequence of books: the i-th book has thickness books[i][0] and height books[i][1].

We want to place these books in order onto bookcase shelves that have total width shelf_width.

We choose some of the books to place on this shelf (such that the sum of their thickness is <= shelf_width), then build another level of shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down. We repeat this process until there are no more books to place.

Note again that at each step of the above process, the order of the books we place is the same order as the given sequence of books. For example, if we have an ordered list of 5 books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.

Return the minimum possible height that the total bookshelf can be after placing shelves in this manner.

Example:

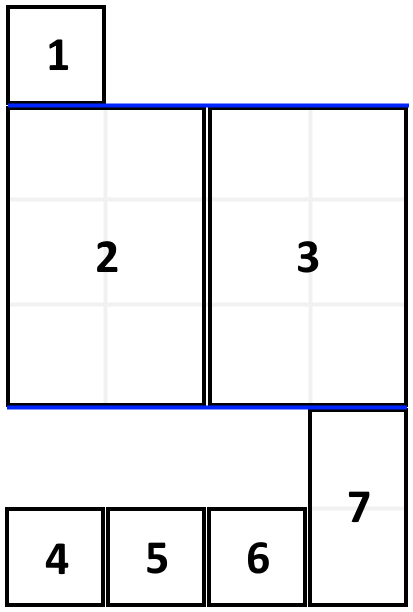
Input: books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelf_width = 4
Output: 6
Explanation:
The sum of the heights of the 3 shelves are 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.

The full description of this problem can be viewed on Leetcode platform filling book case shelves

How to solve this problem ?

The trival way to think this problem is explore all the combination of books and find the optimal solution(brute-fore way). That is going to be exponential time complexity which is not desirable.

Notice there is one important constraint which is the order of the books we place is the same order as the given sequence of books. This means that what we can do is only to place books in order. Then, another solution may occur,we could use backtracking algorithm with branch and bound. To be specific, we could treat all the combinations of placement of books as a recursion tree. We could memorize some previous states for later traverse. Traversing the recursion tree is going to be in the manner of depth-first search.

The codeo of backtracking way for solving this problem is as follows:

class Solution{

    //using cache to memorize intermediate states
    //1st-dim : number of books + 1;
    //2ed-dim : number of shelf_width+1
    private int[][] cache;

    public int minHeightShelves(int[][] books, int shelf_width) {
        cache = new int[books.length+1][shelf_width+1];
        return dfs(books, 0, shelf_width, 0, shelf_width);
    }

    /*
     * @parameters:
     * cur: cur bookIdx
     * widthLeft: left width for the level where cur book is 
     * curHeight: current  height at the layer of cur book 
     */
    public int dfs(int[][] books, int cur, int widthLeft, int curHeight, int shelf_width){
        // if we have explore all books.
        if(cur==books.length){
            return curHeight;
        }

        // if we have traversd the state before , just return. 
        if(cache[cur][widthLeft]!=0) return cache[cur][widthLeft];


        //Option one: 
        // No matter whether the curretn layer if full,  we could place the current  book in the next layer , and explore 
        cache[cur][widthLeft] = curHeight + dfs(books,cur+1,shelf_width-books[cur][0],books[cur][1],shelf_width); 

        // Option two:
        // if the current layer can afford that book. explore with new widthLeft, and 
        // update current height.
        if(widthLeft>=books[cur][0]){
            cache[cur][widthLeft] = Math.min(dfs(books,cur+1,widthLeft-books[cur][0],Math.max(curHeight,books[cur][1]),shelf_width),cache[cur][widthLeft]);
        }
        return cache[cur][widthLeft];
    }
}

To make the code more simple, we could try to optimize the solution by dynamic programming ? How can we think about that? Using an array with length equals to the size of books plus one for storage of the current optimal(minimal) height of the first i-th books. The state function is going to be either it can be put in the new level or, it can merge with previous books One by One as a unit until no extra space left.These two options are the same as the DFS solution.

Here is the code with full comments

class Solution {
    public int minHeightShelves(int[][] books, int shelf_width) {

        //for storage of the current optimal(minimal) height of the first i-th books
        int[] dp = new int[books.length+1];

        // init value: with no book, the optimal height is 0; 
        dp[0] = 0;

        //iterate through all books
        for(int idx = 1; idx < dp.length; idx++){
            // current book height and width
            int height = books[idx-1][1];
            int width = books[idx-1][0];

            // Option 1: place book idx-th on a new shelve 
            dp[idx] = dp[idx-1] + height;

            //Option 2: try to place on the previous shelf with the constraint of width
            for(int j = idx-1; j >0 &&  width + books[j-1][0] <= shelf_width; j--){
                height = Math.max(height, books[j-1][1]);// merge with previous book, height might change
                width += books[j-1][0];// update width
                dp[idx] = Math.min(dp[idx],dp[j-1] + height); // update optimal solution if it is the optimal
            }
        }

        return dp[books.length];

    }
}