Leetcode 1104 Path in Zigzag Labelled Binary Tree

1. Problem Description

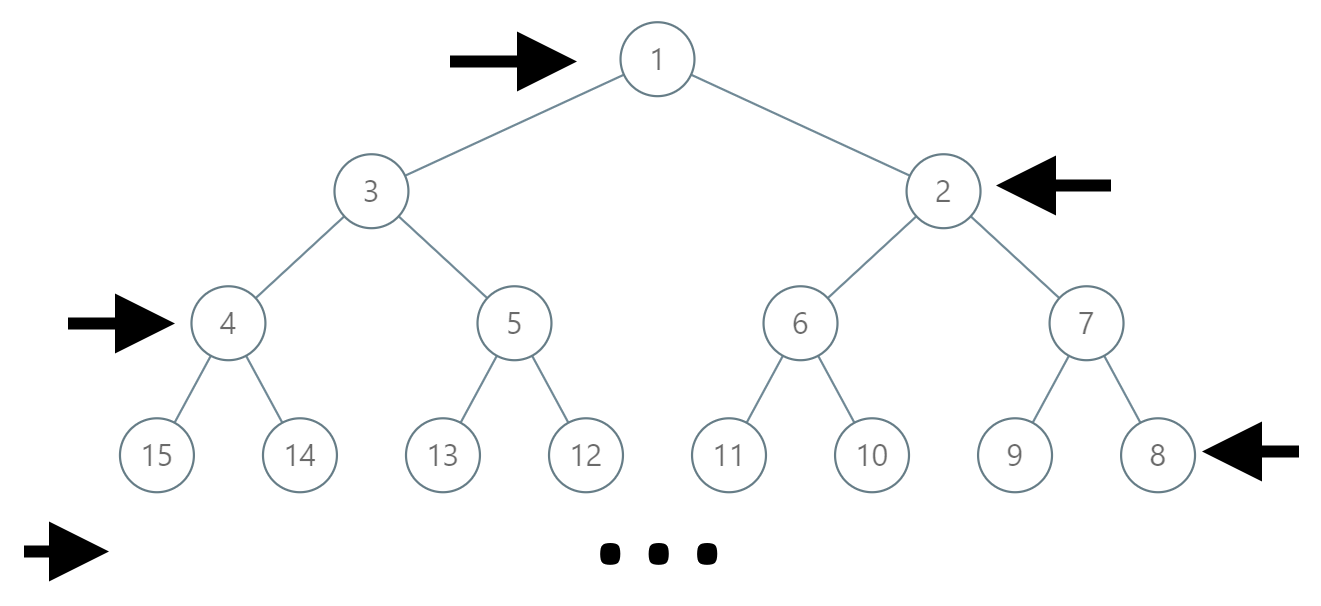
In an infinite binary tree where every node has two children, the nodes are labelled in row order.

In the odd numbered rows (ie., the first, third, fifth,…), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,…), the labelling is right to left.

Challenge:

Given the label of a node in this tree, return the labels in the path from the root of the tree to the node with that label.

Example 1:

Input: label = 14
Output: [1,3,4,14]

Example 2:

Input: label = 26
Output: [1,2,6,10,26]

2. My Thought About This Problem:

Tree data structure itself is recursive, Hence, Many problems regarding to tree can be solved recursively. In this problem, we could think that in order to find the path of the label of a node, how about finding the label of its parent node in the first place. If we can do that, the problem can be solved recursively, until the root node which has label of 1.

3. Difficulty: find the label of its parent node

The tough thing here is to find the label of its parent node. What conditions we have not used yet? Well, the binary tree is complete, and the trees label is in ZigZag Order.

The tree is binary and complete:

1. Given the label, we could compute the depth of the tree by taking the logrithm of two. Let us say the result is k. Then, we also know the range of that level, which is
   [$2^k$, $2^{k+1}$-1].

2. According to ZigZag property, we know that the largest element in the previous layer follows by the smallest element of the current layer.Therefore, we know that the smallest element in the previous layer is $2^k$ - 1.

3.If we could know the difference between the smallest element in the previous and its parent, then we can derive its parent label !

4. Now we only have one condition haven’t applied, which is the tree is complete. Recall that, Heap itseulf is a complete binary tree but it can be stored in an array. The parent of a node with index i in heap is array[i/2]. The offset of current node divides two is the difference we want.

By previous analysis, the code is relatively easy to write.

class Solution {
    public  List<Integer> pathInZigZagTree(int label){
        List<Integer> list = new ArrayList<>();
        bottom2upTraverse(list, label);
        return list;
    }

    private static void bottom2upTraverse(List<Integer> list, int label){
        list.add(0,label);
        if(label == 1) return ;
        // get the level of the label in the tree;
        int level = log2(label);

        // get the index of the label on its level
        int idx = label - (int) Math.pow(2,level);

        // according to ZigZag Tree property, find the previous label to traverse;
        int nextLabel = (int) Math.pow(2,level) - 1 - idx/2;

        // traverse recursively.
        bottom2upTraverse(list,nextLabel);
    }

    private static int log2(int n) {
        return (int)(Math.log(n) / Math.log(2));
    }
}